3. Trigonometry

c. Circle Definitions

1. Formulas

The triangle definitions of the trig functions are perfectly fine if the angle \(\theta\) is between \(0^\circ\) and \(90^\circ\) (or \(0\) rad and \(\dfrac{\pi}{2}\) rad). However, it doesn't make any sense if \(\theta\) is outside this range. So we generalize it using a circle.

In both circles at the right, the radius is \(r\) and the radial line at an angle \(\theta\) counterclockwise from the positive \(x\)-axis passes through the circle at a point \(P\) whose coordinates are \(P=(x,y)\). If we drop a perpendicular from \(P\) to the \(x\)-axis, we get a right triangle whose legs are \(|x|\) and \(|y|\) and whose hypotenuse is \(r\). In the \(1^\text{st}\) quadrant, \(x\) and \(y\) are the adjacent and opposite sides of the triangle needed for the definition of the trig functions and the absolute values are not necessary. In the other quadrants, we still replace the adjacent and opposite sides by \(x\) and \(y\) and we still don't put in any absolute values. So in any quadrant, the six trig functions Sine  Cosine Tangent  Cotangent Secant  Cosecant are defined to be: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}\quad &\cos\theta&=\dfrac{x}{r} \\[8pt] \tan\theta&=\dfrac{y}{x}\quad &\cot\theta&=\dfrac{x}{y} \\[8pt] \sec\theta&=\dfrac{r}{x}\quad &\csc\theta&=\dfrac{r}{y} \end{aligned}\]

Memorize this!

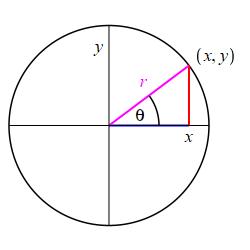
def_FirstQuadrant
\(\theta\) is in the \(1^\text{st}\) quadrant



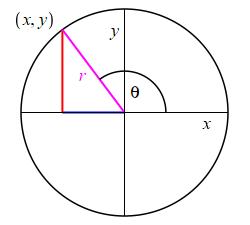
def_SecondQuadrant
\(\theta\) is in the \(2^\text{nd}\) quadrant

Conversely, we have

If \((x,y)\) is the point on a circle with radius \(r\) at angle \(\theta\) then its coordinates are \[ x=r\cos\theta \qquad \text{and} \qquad y=r\sin\theta \] The ordered pair \((r,\theta)\) is called the Polar Coordinates of the point \((x,y)\).

The quotient and reciprocal identities are unchanged:

\[\begin{aligned} &\tan\theta=\dfrac{\sin\theta}{\cos\theta}\quad &&\cot\theta=\dfrac{\cos\theta}{\sin\theta}=\dfrac{1}{\tan\theta} \\[8pt] &\sec\theta=\dfrac{1}{\cos\theta}\quad &&\csc\theta=\dfrac{1}{\sin\theta} \end{aligned}\]

Trig Functions at Standard Angles

It is easy to remember values of \(\sin\), \(\cos\) and \(\tan\) for the five standard angles \[ 0^\circ=0 \,\text{rad}, \qquad 30^\circ=\dfrac{\pi}{6} \,\text{rad}, \qquad 45^\circ=\dfrac{\pi}{4} \,\text{rad}, \qquad \] \[ 60^\circ=\dfrac{\pi}{3} \,\text{rad} \qquad \text{and} \qquad 90^\circ=\dfrac{\pi}{2} \,\text{rad} \]

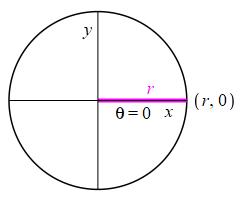
For \(\theta=0\,\text{rad}\,=0^\circ\), the radial line is horizontal and so \(x=r\) and \(y=0\). So \[ \sin 0=0 \quad \cos 0=1 \quad \text{and} \quad \tan 0=0 \]

eg_theta=0

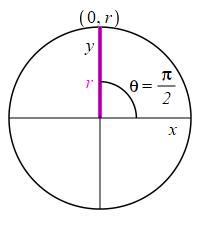
For \(\theta=\dfrac{\pi}{2}\,\text{rad}\,=90^\circ\), the radial line is vertical and so \(x=0\) and \(y=r\). So \[ \sin \dfrac{\pi}{2}=1 \quad \cos \dfrac{\pi}{2}=0 \quad \text{and} \quad \tan \dfrac{\pi}{2}=\pm\infty \]

eg_theta=90

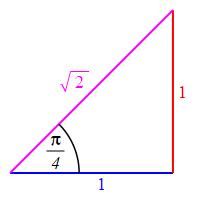
For \(\theta=\dfrac{\pi}{4}\,\text{rad}\,=45^\circ\), \(x=y\) and the Pythagorean Theorem says the hypotenuse is: \[ r=\sqrt{x^2+y^2}=\sqrt{x^2+x^2}=\sqrt{2}\,x \] If we take \(x=y=1\), then \(r=\sqrt{2}\) and the trig functions are: \[ \sin\dfrac{\pi}{4}=\dfrac{1}{\sqrt{2}} \quad \cos\dfrac{\pi}{4}=\dfrac{1}{\sqrt{2}} \quad \text{and} \quad \tan\dfrac{\pi}{4}=1 \] Don't Memorize the trig functions!
Memorize the sides of a \(45^\circ\) right triangle are

\(1\), \(1\), \(\sqrt{2}\) or “one, one, the square root of two”
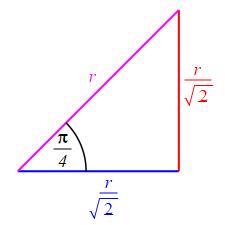
If we need the hypotenuse to be \(r\), then we multiply by a scale factor \(\dfrac{r}{\sqrt{2}}\).

eg_45degTriangle
eg_45degTriangleRadiusR

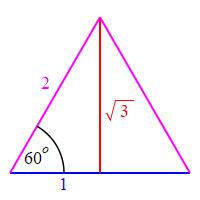
For \(\theta=\dfrac{\pi}{6}\,\text{rad}\,\) and \(\theta=\dfrac{\pi}{3}\,\text{rad}\,\), we need to know the ratio of the sides of a \(30^\circ-60^\circ-90^\circ\) right triangle. Consider an equilateral triangle and drop a perpendicular from one vertex to the opposite side splitting the triangle into two halves. Since the angles of the equilateral triangle are all \(60^\circ\), the half triangle is a \(30^\circ-60^\circ-90^\circ\) right triangle. 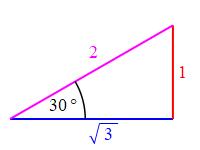If the side of the equilateral triangle is \(2\), then the base of the half triangle is \(b=1\) and its altitude is \[ a=\sqrt{2^2-1^2}=\sqrt{3} \] We usually remember the sides of a \(30^\circ-60^\circ-90^\circ\) right triangle as: \(1\), \(2\), \(\sqrt{3}\) or “one, two, the square root of three”
Notice that the smallest angle (\(30^\circ\)) is opposite the smallest side (\(1\)) and the largest angle (\(90^\circ\)) is opposite the largest side (\(2\)).

If we need the hypotenuse to be \(r\), then we multiply by a scale factor \(\dfrac{r}{2}\). Consequently:

eg_Equilateral


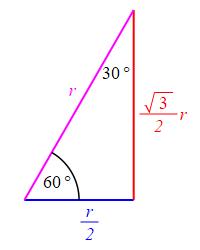
eg_EquilateralRadiusR

For \(\theta=\dfrac{\pi}{6}\,\text{rad}\,=30^\circ\), the trig functions are: \[ \sin\dfrac{\pi}{6}=\dfrac{1}{2} \quad \cos\dfrac{\pi}{6}=\dfrac{\sqrt{3}}{2} \quad \text{and} \quad \tan\dfrac{\pi}{6}=\sqrt{3} \]

eg_theta=30

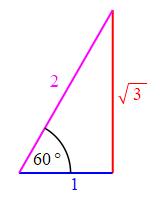
For \(\theta=\dfrac{\pi}{3}\,\text{rad}\,=60^\circ\), the trig functions are: \[ \sin\dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2} \quad \cos\dfrac{\pi}{3}=\dfrac{1}{2} \quad \text{and} \quad \tan\dfrac{\pi}{3}=\dfrac{1}{\sqrt{3}} \]

eg_theta=60

Don't Memorize the trig functions!
Memorize the sides of a \(30^\circ-60^\circ-90^\circ\) right triangle are

\(1\), \(2\), \(\sqrt{3}\) or “one, two, the square root of three”

Find the coordinates of the point on the circle of radius \(4\) at \(30^\circ\) from the \(x\)-axis.

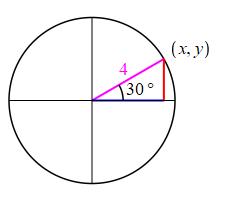
ex_4_30deg

Recall, the coordinates of a point are given by: \[ x=r\cos\theta \qquad \text{and} \qquad y=r\sin\theta \]

\((x,y)=\left(2\sqrt{3},2\right)\)

The coordinates of a point are given by: \[ x=r\cos\theta \qquad \text{and} \qquad y=r\sin\theta \] Since \(\sin30^\circ=\dfrac{1}{2}\) and \(\cos30^\circ=\dfrac{\sqrt{3}}{2}\) and \(r=4\) the point is \[ (x,y)=\left(4\cdot\dfrac{\sqrt{3}}{2},4\cdot\dfrac{1}{2}\right) =\left(2\sqrt{3},2\right) \]

Consider a circle centered at the origin and the ray at the angle \(\theta\) which passes through the point \((4,3)\), find the radius of the circle and identify the six trig functions for the angle \(\theta\).

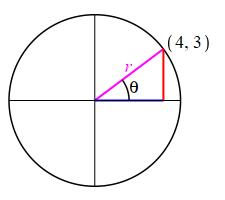
ex_4-3-5

\(r=5\)
\( \sin\theta=\dfrac{3}{5}\quad \tan\theta=\dfrac{3}{4}\quad \sec\theta=\dfrac{5}{4} \)

\( \cos\theta=\dfrac{4}{5}\quad \cot\theta=\dfrac{4}{3}\quad \csc\theta=\dfrac{5}{3} \)

Since the ray at the angle \(\theta\) passes through the point \((x,y)=(4,3)\), the radius is \[ r=\sqrt{4^2+3^2}=\sqrt{16+9}=5 \] So the trig functions are: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}=\dfrac{3}{5}\quad &\tan\theta&=\dfrac{y}{x}=\dfrac{3}{4}\quad &\sec\theta&=\dfrac{r}{x}=\dfrac{5}{4} \\[8pt] \cos\theta&=\dfrac{x}{r}=\dfrac{4}{5}\quad &\cot\theta&=\dfrac{x}{y}=\dfrac{4}{3}\quad &\csc\theta&=\dfrac{r}{y}=\dfrac{5}{3} \end{aligned}\]

© MYMathApps

Supported in part by NSF Grant #1123255